Algebraic algorithms and computing
- Polynomial system solving, sparse/toric elimination theory, structured matrices. Resultants reduce system solving to linear algebra. Newton polytopes provide the bridge between algebra and combinatorial geometry. Optimal sparse resultant matrices for multihomogeneous polynomial systems (article), and MAPLE software MHRES. Macaulay-type formulae for sparse resultants of generalized unmixed systems (article). More Algebraic software.
- Real solving, Real algebraic numbers. Solvers based on Continued Fractions and Sturm sequences. Software tools in C++ (Mathemagix): module Realroot, interval-Newton method, solvers for polynomial systems (subdivision methods). MAPLE software SLV for real algebraic numbers, real solving of equations and bivariate systems. Benchmarking of black-box univariate real solvers.
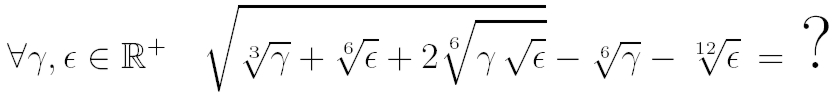
Geometric computing, and Optimization
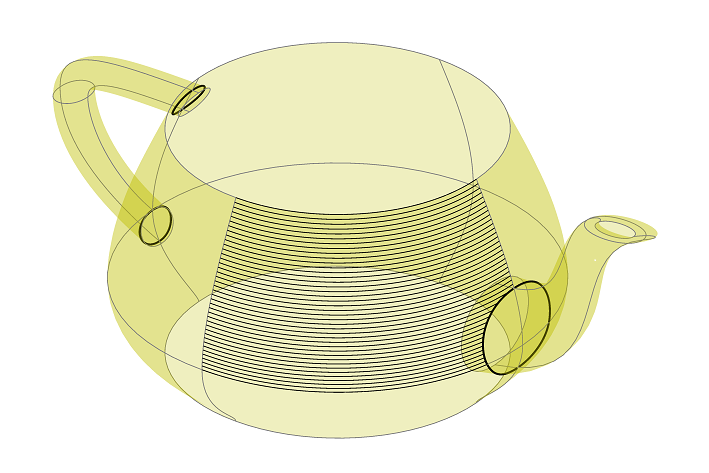
- Geometric Modeling and Nonlinear Computational geometry. Exact and approximate implicitization of parametric hypersurfaces by interpolation using matrix operations, and sparse elimination for exploiting structure (article). Extensions to space curves and objects defined by point clouds (Wiki page). Voronoi diagrams of circles and ellipses (IMA nugget), arrangements of curved objects (talk) on CGAL. Python projects and CGAL-Python bindings, including visibility tools: webpage. Pictured is a teapot modeled using sparse and Bezout resultants (courtesy F. Groh).
- Convex geometry in general dimension. Random walks for sampling convex regions, and for poly-time approximation of polytope volume (C++ and R software). Convex hull and symbolic perturbation, mixed volume (software). Regular fine mixed subdivisions of Minkowski sums, regular triangulations, secondary polytopes, resultant polytopes (software). Minkowski decomposition (webpage): optimal algorithms with a fixed-size summand, approximation of general (NP-hard) problem. Polytopal computations: normals, faces, ridges, extreme or interior points (module Polytopix in Mathemagix).
- Optimization. Geometric optimization and clustering. Combinatorial optimization, capacitated vehicle routing with time windows, matching, bin packing (an example of computed routes in the Figure). Mathematical modeling. Use of Google’s OR-Tools. Collaboration with EmDoT.
Data science and Machine Learning
- Geometric search in high dimensions. kd-GeRaf: Generalized Randomized kd-trees for fast approximate nearest-neighbors of points, in very high dimensions (competitive in dimension of up to 10,000): Web tool, Software, further info. Dimensionality reduction by a weak version of the JL lemma, and record complexity bounds for ANN (SoCG 2015). Software in C++ and Python. Fast, high-dimensional, approximate nets (SODA 2017). Practical applications to data mining of 3D shapes by various encodings, including geometric learning.
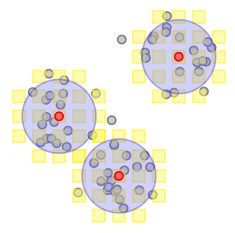
- Clustering algorithms. IQ-means: Clustering for big data: we improve k-means by reverse assignment, combined with ideas from product quantization (image), to cluster 100 Mil SIFT images in 1hr (Software tool IQ-means, paper at ICCV 2015). Applications to 3D objects such as molecular structures and mechanical parts.
- Wind and wind-energy forecasting. We employ Scientific computing for processing open meteorological data (GFS) in creating WRF grid models for large geographic domains (within Greece), then develop original Machine Learning architectures for long-term (48h) prediction of wind speed as well as wind energy. Recurrent Neural Networks (also for cryptocurrency evaluation) capture time dependencies, Convolutional Neural Networks capture geographic structure (grid). Deep learning, transfer learning, ensembles.

Structural bioinformatics and Robotics
For our research in bioinformatics please also visit our dedicated webpage.
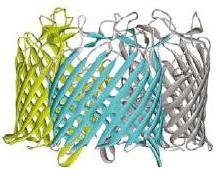
- Structure of Transmembrane proteins. Geometric modelling of β-barrels and detection of the transmembrane region of a β-barrel transmembrane protein. Given a PDB file, the transmembrane region is detected by profiling the external residues of the β-barrel along its axis in terms of hydrophobicity and existence of aromatic and charged residues. Our geometric modeling of the barrel relies on combining nonlinear least square minimization and a genetic algorithm. TbB-Tool is the software tool. Paper.
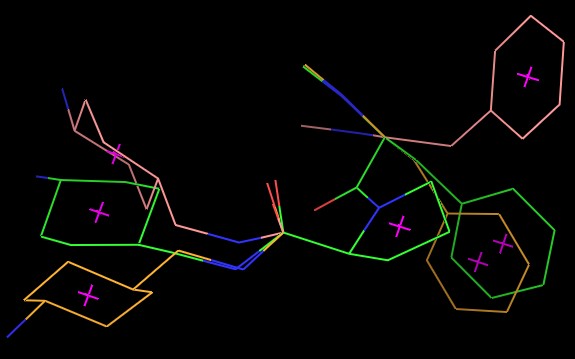
- Molecular conformations in Structural bioinformatics. Enumeration of all possible conformations of (small) molecules/proteins under geometric constrains; C-Space (interactive example). Paper by Emiris, Fritzilas, Manocha. Sampling of rotamers, and clustering to deduce structural determinants. Graph embedding in Euclidean spaces, rigidity theory, enumerative problems of embeddings, distance geometry to compute conformations from NMR data.
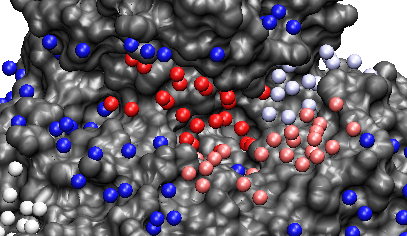
- Lakes is a software tool for the prediction of protein binding sites. It analyzes the solvent and its contacts with proteins and defines clusters of water molecules, which mark potentially exposed interaction and binding sites of the protein. Contact: Dr Thanassis Tartas. Figure: black is the protein, colored are the oxygen atoms of clusters, red being the largest cluster.
- Robot kinematics. Robust calibration of parallel robots (by applying elimination techniques), forward kinematics of Stewart/Gough platforms, and design of robotic platforms for medical applications such as physiotherapy.
