Research Topics
For immediate openings look under News: an 8.5-month Marie-Curie fellowship is currently available in Geometric Learning, for students holding a MSc degree. PhD, MSc, and BSc theses can be undertaken in all of our Lab’s topics (details below), or in the framework of existing projects. Here is some administrative info for PhD students and instructions on applying for BSc/MSc theses (in Greek).
Geometric computing / Geometric modeling

- Sampling and volume estimation of (non)linear (non)convex regions (volesti software) by poly-time methods. Applications include scoring financial portfolios (our paper), and forecasting market crises via copulas.
- There are various useful representations of geometric objects, most notably implicit, parametric, and point clouds. We develop efficient ways for switching between representations while exploiting properties such as sparseness.
- Voronoi diagrams of complex objects and the corresponding algebraic operations for constructing them. Large datasets, nonlinear objects and applications (paper for ellipses).
Machine Learning
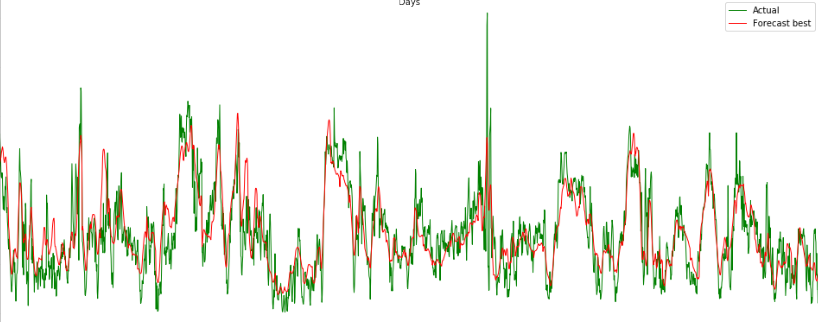
- Approximate Nearest Neighbors (ANN) and randomized projections (following our first paper): Queries lying in a subspace (bio data); ANN on complex 1D objects, e.g. time series, exploit time parameter (vs. Frechet distance as in our paper); experimental validation of the Dolphinn approach; farthest directional neighbor.
- Clustering of complex objects (representation via Neural Networks), IQ-Means algorithm.
- Deep geometric learning for 3d shapes (representation, mining, classification, segmentation).
Algebraic algorithms / polynomials

- Discrete geometry for capturing and exploiting algebraic properties. Mixed volume and root bounds via the Permanent.
- Approximate Mixed volume via the volume approximation methods (telescoping method on mixed cells or fraction of “mixed” sample); sample of mixed cells for MV estimation and sample of root homotopies.
- Polynomial system solving by linear algebra. Sparse resultants and Macaulay formulae. Structured systems such as multi-homogeneous systems.
Bioinformatics
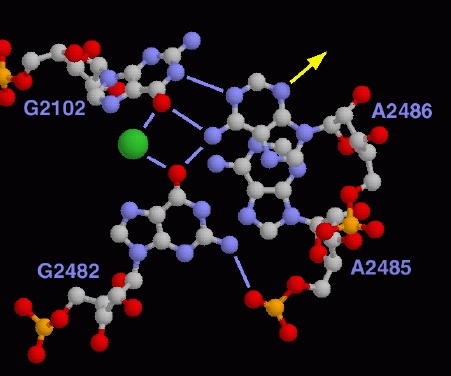
- Molecular 3d structure, folding. Cryo-EM. Geometric, statistical (sampling).
- Docking, Rotamers and Geometric Learning.
- Rigidity theory (counting rigid graphs), and Distance geometry on NMR data for ab initio structure prediction (in Greek).
Robotics

- Parallel and wire robots, kinematics, calibration, collision avoidance. Applications to molecular kinematics
- Distance geometry and pose counting. Over-constrained algebraic systems and applications in calibration.